Calculadora de margen de error: fórmula y ejemplos
Usa nuestra precisa calculadora en línea para medir tu margen de error al instante.
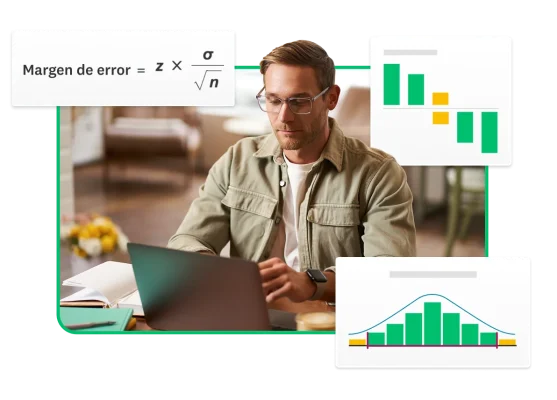
- El margen de error indica la incertidumbre en los resultados de la encuesta y muestra cuánto pueden diferir los resultados de la muestra de la población total.
- El margen de error se calcula con los siguientes elementos: n = tamaño de la muestra • σ = desviación estándar de la población • z = puntuación z (también puedes usar la calculadora a continuación).
- La calculadora de margen de error te ayudará a determinar si el tamaño de tu muestra es suficiente para confiar en la exactitud de los datos que recopilas.
Calcula tu margen de error
Tamaño de la población
Nivel de confianza (%)
Tamaño de la muestra
Margen de error
0
¿Qué es un margen de error?
Encuestar es un acto de equilibrio en el que utilizas un pequeño grupo (tus encuestados) para representar a una población mucho más grande (el mercado objetivo o población total). El margen de error es una medida estadística de con qué precisión los resultados de una encuesta reflejan las opiniones de toda la población.
En pocas palabras, mide la precisión de tu encuesta. Cuanto menor sea el margen de error, más confianza puedes tener en los resultados. Cuanto mayor sea el margen de error, más se desviarán de las opiniones de la población total.
El margen de error es un rango de valores acerca de los resultados de la encuesta. Por ejemplo, un 60 % de respuestas “sí” con un margen de error del 5 % y un nivel de confianza del 95 % significa que existe un 95 % de probabilidades de que entre el 55 % y el 65 % de la población responda “sí”.
El margen de error es fundamental en las investigaciones y encuestas porque nos indica qué tan confiables son los resultados. Nos ayuda a comprender el grado de incertidumbre en nuestros hallazgos y sirve para guiar nuestra interpretación de los datos. Un margen de error más pequeño indica una mayor precisión y confianza en los resultados, mientras que un margen más grande sugiere más variabilidad y menos certeza.
En última instancia, conocer el margen de error permite a los investigadores y a los responsables de tomar decisiones emitir juicios informados en función de la confiabilidad de los datos.
¿Qué es un intervalo de confianza?
Los intervalos de confianza proporcionan una forma de calcular el rango dentro del cual creemos que se encuentra el resultado real. Por ejemplo, si queremos calcular la estatura promedio de todos los adultos en un país, un intervalo de confianza nos da un rango de estaturas que estamos bastante seguros de que incluye el verdadero promedio.
Los intervalos de confianza ayudan a los investigadores y a los responsables de tomar decisiones a comprender la incertidumbre asociada con sus cálculos y análisis.
Cómo se relaciona el margen de error con los intervalos de confianza
Los intervalos de confianza y el margen de error básicamente son dos formas diferentes de expresar el mismo concepto: la incertidumbre en torno a la estimación de una encuesta. El intervalo de confianza proporciona un rango de valores dentro del cual creemos que se encuentra el resultado real. El margen de error proporciona una medida específica de cuánto puede desviarse la estimación del valor real.
Un concepto relacionado aunque diferente es el nivel de confianza. Este nos indica qué tan probable es que el valor real se encuentre dentro del intervalo.
Los niveles de confianza comunes incluyen 90 %, 95 % y 99 %. Un nivel de confianza más bajo, como 90 %, nos dará un intervalo de confianza más estrecho. Cuanto más estrecho sea el intervalo, más precisa será nuestra estimación, pero usar un nivel de confianza más bajo significa que es menos probable que este registre el valor real. Por el contrario, un nivel de confianza más alto, como 99 %, nos dará un intervalo de confianza más amplio. Este intervalo más amplio será menos preciso, pero es más probable que incluya el valor real.
Cuándo usar un margen de error

Úsalo en la planificación de tu encuesta para asegurarte de obtener resultados precisos y confiables. Comprender el margen de error te permitirá calcular el tamaño de la muestra que necesitas para lograr el nivel deseado de precisión en los resultados de tu encuesta. Un margen de error más pequeño requiere un tamaño de muestra más grande, mientras que un margen de error más grande permite que el tamaño de la muestra sea más pequeño.
Por ejemplo, si un investigador desea realizar una encuesta en una población de 100 000 personas con un margen de error de ±5 % y un nivel de confianza del 95 %, necesitaría un tamaño de la muestra de aproximadamente 383 encuestados, calculado mediante fórmulas estándar.
Asimismo, un margen de error es fundamental en la interpretación de los hallazgos de la encuesta. Proporciona una medida de la incertidumbre en los resultados y permite que los investigadores y las partes interesadas evalúen la confiabilidad de las conclusiones.
Por ejemplo, si una encuesta informa que el 60 % de los encuestados prefiere el producto A al producto B, con un margen de error de ±3 % y un nivel de confianza del 95 %, significa que hay una alta probabilidad (95 %) de que la verdadera proporción de personas que prefieren el producto A se encuentre entre el 57 % y el 63 %.
¿Cuál es la fórmula para calcular el margen de error?
La fórmula utilizada para calcular el margen de error es la siguiente:

n = tamaño de la muestra • σ = desviación estándar de la población • z = puntuación z
- Obtén la desviación estándar de la población (σ) y el tamaño de la muestra (n). La calculadora que está al inicio de la página asume una desviación estándar basada en la raíz cuadrada de p(1-p), donde p es la proporción de la muestra y p=0.5 es un valor predeterminado conservador.
- Divide la desviación estándar de la población entre la raíz cuadrada del tamaño de la muestra.
- Multiplica el resultado por la puntuación z de acuerdo con el nivel de confianza deseado tomando en cuenta la siguiente tabla:
| Nivel de confianza deseado | Puntuación z |
| 80 % | 1.28 |
| 85 % | 1.44 |
| 90 % | 1.65 |
| 95 % | 1.96 |
| 99 % | 2.58 |
Ejemplo de cálculo del margen de error
Imagínate que estás intentando decidir entre el nombre A y el nombre B para un nuevo producto y tu mercado objetivo consta de 400 000 clientes potenciales; esta es tu población total.
Decides encuestar a 600 de esos clientes potenciales; este es el tamaño de la muestra.
Cuando obtienes los resultados, el 60 % de los encuestados dice que prefiere el nombre A. Necesitas ingresar un nivel de confianza en la calculadora de margen de error.
Este número expresa cuánta certeza tienes de que la muestra refleja con precisión las actitudes de la población total. Los investigadores generalmente la establecen en 90 %, 95 % o 99 %.
Si ingresas los números de este ejemplo en la calculadora que está más arriba, te proporcionará un margen de error del 4 %.
¿Recuerdas que el 60 % de los encuestados eligió el Nombre A? Este margen de error significa que ahora sabes con un 95 % de confianza que entre el 56 % y el 64 % de la población total (tu mercado objetivo) prefiere el Nombre A para tu producto.
Obtenemos 56 y 64 al sumar y restar el margen de error de la respuesta de tu muestra.
Cómo interpretar el margen de error
El margen de error es un rango de valores acerca de los resultados de la encuesta, el cual muestra el nivel de incertidumbre. Por ejemplo, si una encuesta indica que el 60 % apoya una política con un margen de error de ±4 % con un nivel de confianza del 95 %, estamos razonablemente seguros de que el nivel de apoyo verdadero se encuentra entre el 56 % y el 64 %.
Factores que influyen en el margen de error
1. Tamaño de la muestra
El tamaño de la muestra repercute directamente en el margen de error en las encuestas. Las muestras más grandes suelen dar lugar a márgenes de error más pequeños, y las muestras más pequeñas dan lugar a márgenes de error más grandes.
Por ejemplo, una encuesta con 1000 encuestados podría tener un margen de error de ±3 %. Duplicar el tamaño de la muestra a 2000 podría reducir el margen de error a ±2 %.
Lectura relacionada: Calculadora del tamaño de la muestra
2. Nivel de confianza
Los niveles de confianza más altos dan como resultado márgenes de error más amplios. Los niveles de confianza más bajos dan lugar a márgenes de error más limitados.
Por ejemplo, una encuesta con un nivel de confianza del 95 % podría tener un margen de error de ±3 %, mientras que aumentar el nivel de confianza al 99 % podría dar como resultado un margen de error de ±4 %.
3. Variabilidad de la población
Una mayor variabilidad de la población conduce a mayores márgenes de error, y una menor variabilidad da como resultado márgenes más pequeños.
Por ejemplo, estimar los ingresos en una ciudad que presenta grandes diferencias de ingresos puede requerir un margen de error mayor, como ±USD 5000. En comparación, una ciudad con ingresos más homogéneos puede darte un margen más pequeño, como ±USD 2000.
Cómo incrementar la confiabilidad de tus datos

Ahora que ya conoces cómo se calcula el margen de error y cómo afecta tus resultados, revisemos los pasos que debes seguir para utilizar estos conceptos en el diseño de tu encuesta.
1. Define tu población total
Esta es el conjunto completo de personas que deseas estudiar con tu encuesta, es decir, los 400 000 clientes potenciales del ejemplo anterior.
2. Decide el nivel de riesgo
Necesitas decidir cuánto riesgo estás dispuesto a correr con respecto al hecho de que tus resultados difieran de las actitudes del mercado objetivo total. Esto significa medir el margen de error y el nivel de confianza de tu muestra.
3. Especifica la muestra
Después de equilibrar el nivel de confianza que deseas obtener y el margen de error que consideras aceptable, tu siguiente decisión es cuántos encuestados necesitarás. Además, no olvides que no todos los que reciben la encuesta la responderán: el tamaño de la muestra es el número de respuestas completas que obtienes.
4. Calcula el índice de respuestas
Este es el porcentaje de encuestados que sí respondieron tu encuesta entre quienes la recibieron. Puedes observar tus encuestas anteriores para comprobar cuál es tu índice habitual. Si no tienes datos de encuestas anteriores, haz una conjetura bien fundamentada. Una conjetura conservadora es que aproximadamente entre el 10 % y el 15 % completará la encuesta.
5. Encuesta a tu público objetivo
Una vez que conozcas el porcentaje del Paso 4, sabrás a cuántas personas necesitas enviar la encuesta para obtener suficientes respuestas completadas del Paso 3. Como hemos visto, conocer tu margen de error (y todos los conceptos relacionados como el tamaño de la muestra y el nivel de confianza) es una parte importante del acto de equilibrio de diseñar una encuesta. Calcularlos te permitirá continuar con seguridad.
Lectura relacionada: Cómo estimar tu población
Mejora tu margen de error con SurveyMonkey
Aumenta el tamaño de tu muestra y reduce el margen de error con SurveyMonkey. SurveyMonkey Audience ofrece una potente plataforma para recopilar datos de alta calidad con rapidez y eficiencia de un público que refleja tu mercado objetivo. Ya sea que quieras lanzar un nuevo producto, medir la satisfacción de los clientes o realizar una investigación académica, nuestra plataforma te brinda las herramientas que necesitas para llegar a tu público objetivo y obtener respuestas significativas.
Recopila los datos correctos
SurveyMonkey te brinda las herramientas que necesitas para crear, optimizar y compartir tus encuestas y que recopiles las respuestas que necesitas.